The codes in this section are published for pedagogical purposes only. Teachers of advanced university-level courses in solid mechanics and dynamics are welcome to refer to these codes. Please do not use them for any commercial use or publish them on any other online platform. Write to me at dipayanm@iitk.ac.in in case you have any question, suggestion, bug-fix, etc.
-
3D rolling of rigid bodies I: Spin reversal of the Rattleback

Rattleback is an ellipsoidal solid that has a “preferred direction” of rotation as shown by the simulations. Notice for Case II that the ellipsoid is reversing its direction of rotation from counter-clockwise to its preferred clockwise direction about the vertical axis. A table-top experiment with this toy can be viewed in this YouTube video.
The formulation and Matlab code simulating the “Rattleback Reversal” is here: rattleback_simulator.zip
In this simulation, I have used the principles of 3-dimensional rigid body dynamics (taught in ME209A and ME625A at IITK).
-
3D rolling of rigid bodies II: “Standing up” of spinning hard-boiled eggs
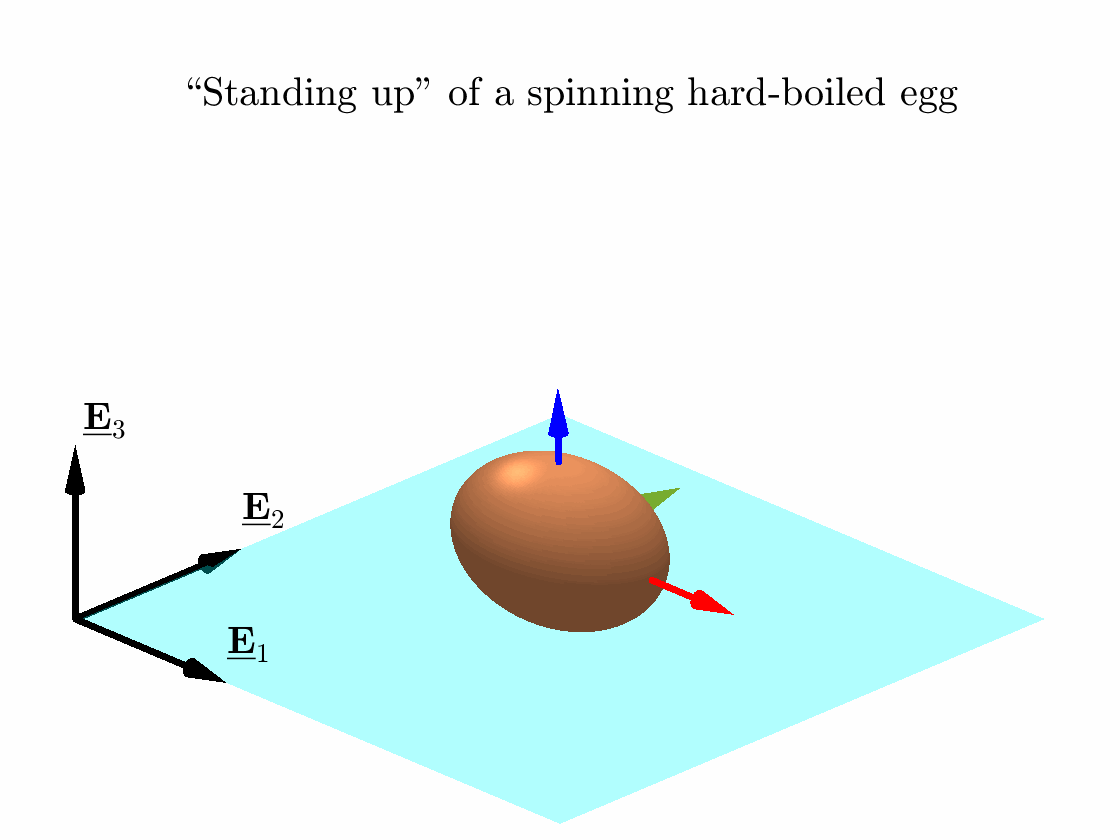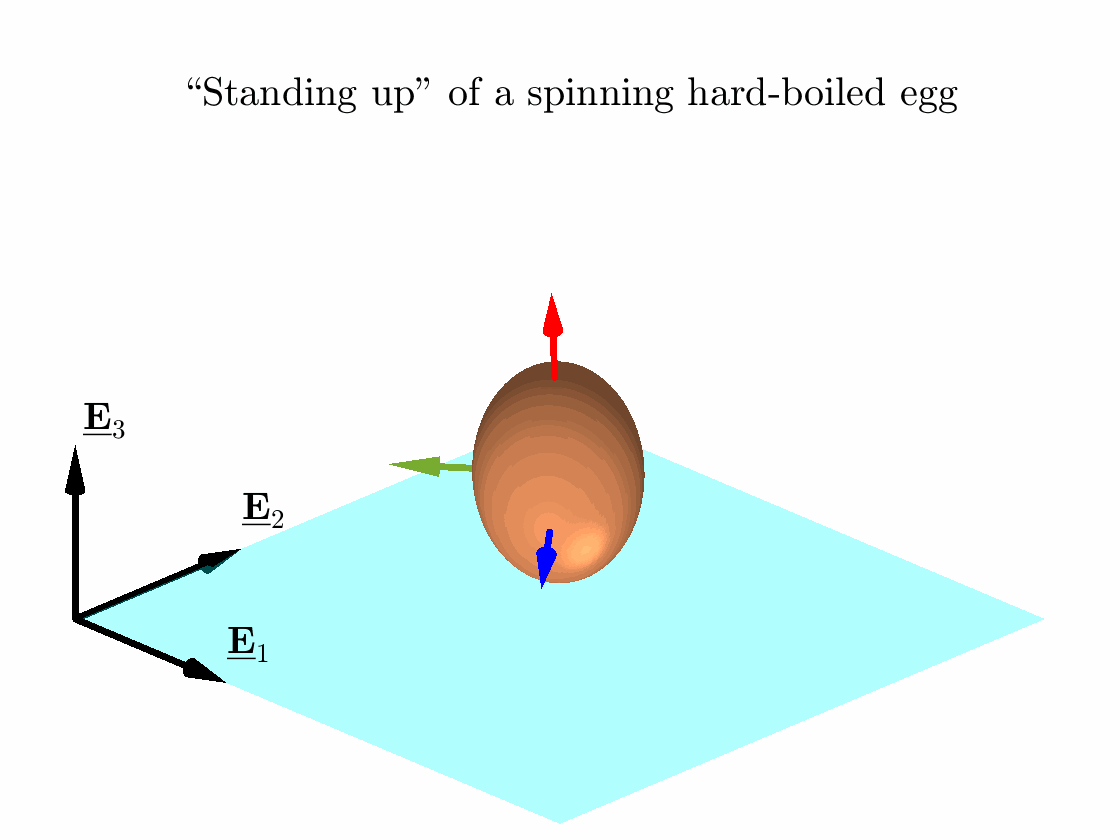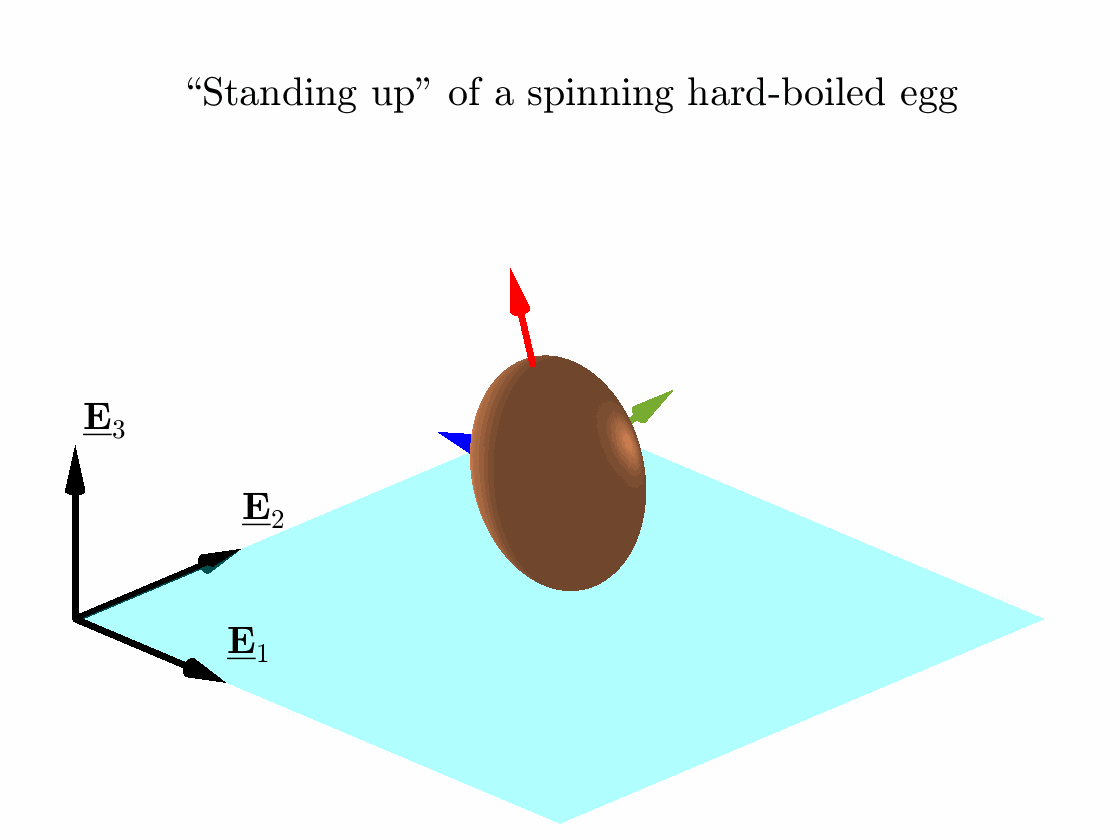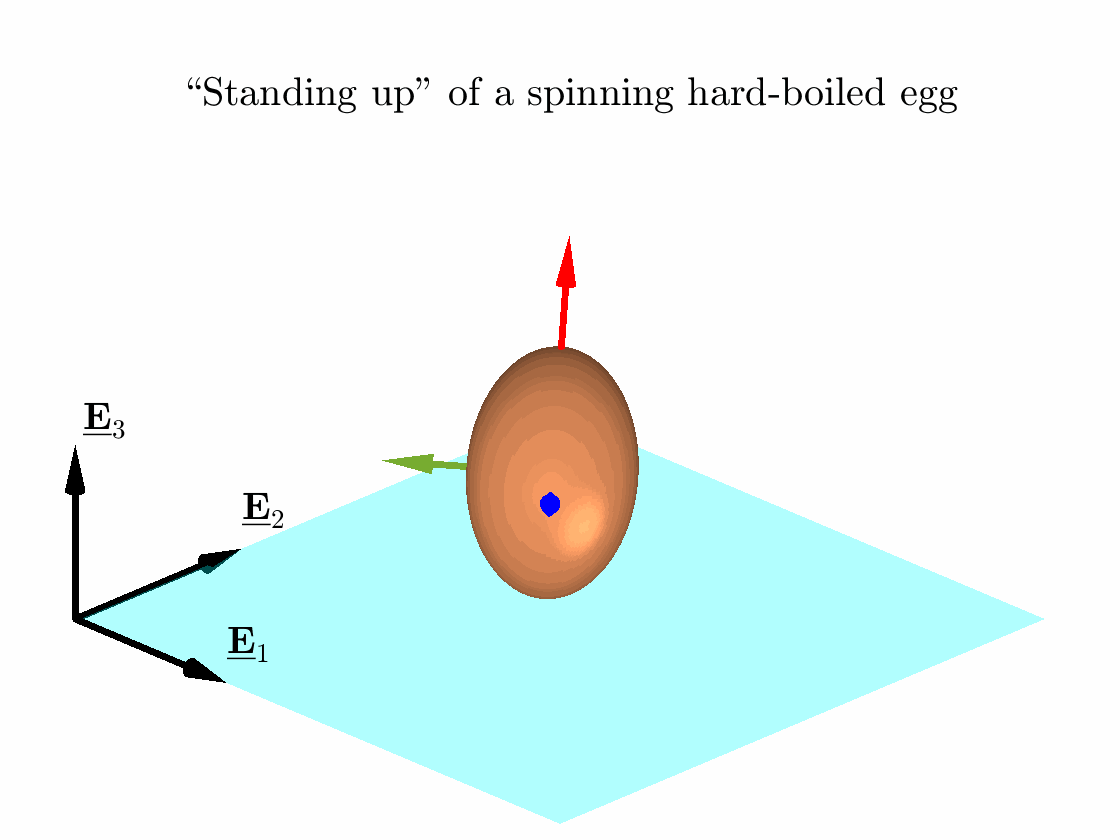
Hard-boiled eggs prefer rotating about its longer axis when spun on a rough flat surface initially keeping its longer axis horizontal; see, e.g., this video. The attached code simulates this “standing up” phenomena as shown in the animation. I have assumed the hard-boiled egg to be a perfectly rigid body and used the classical Newton-Euler approach to model its motion.
The classical Newton-Euler mechanics-based formulation and a Matlab code simulating the “Rising egg” is here: Rising_egg_code.zip
Prerequisite courses: Dynamics of rigid bodies (ME209A and ME625A at IITK).
-
3D rolling of rigid bodies III: Inversion of the Tippe-top
Tippe-tops are known for their inversion upon spinning. The initial spin is given to its stem keeping it pointing upwards. However, the top prefers rotating on its stem and thus inverses its configuration shortly after the initial spin. See this YouTube video for example. Here also I have used the classical Newton-Euler approach to model this rotating rigid body.
The formulation and a Matlab code simulating the Tippe-top inversion is here: Tippe_top_code.zip
Prerequisite courses: Dynamics of rigid bodies (ME209A and ME625A at IITK).
-
Geometrically-exact, pre-magnetized flexible beams
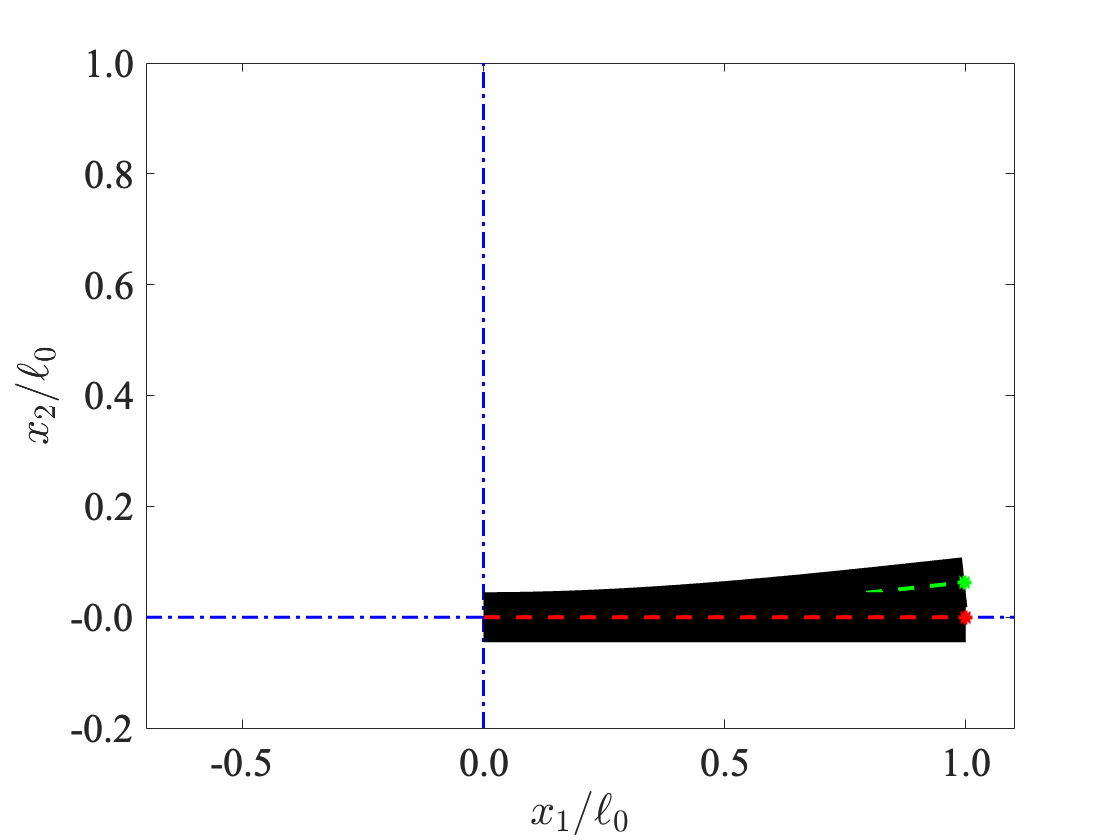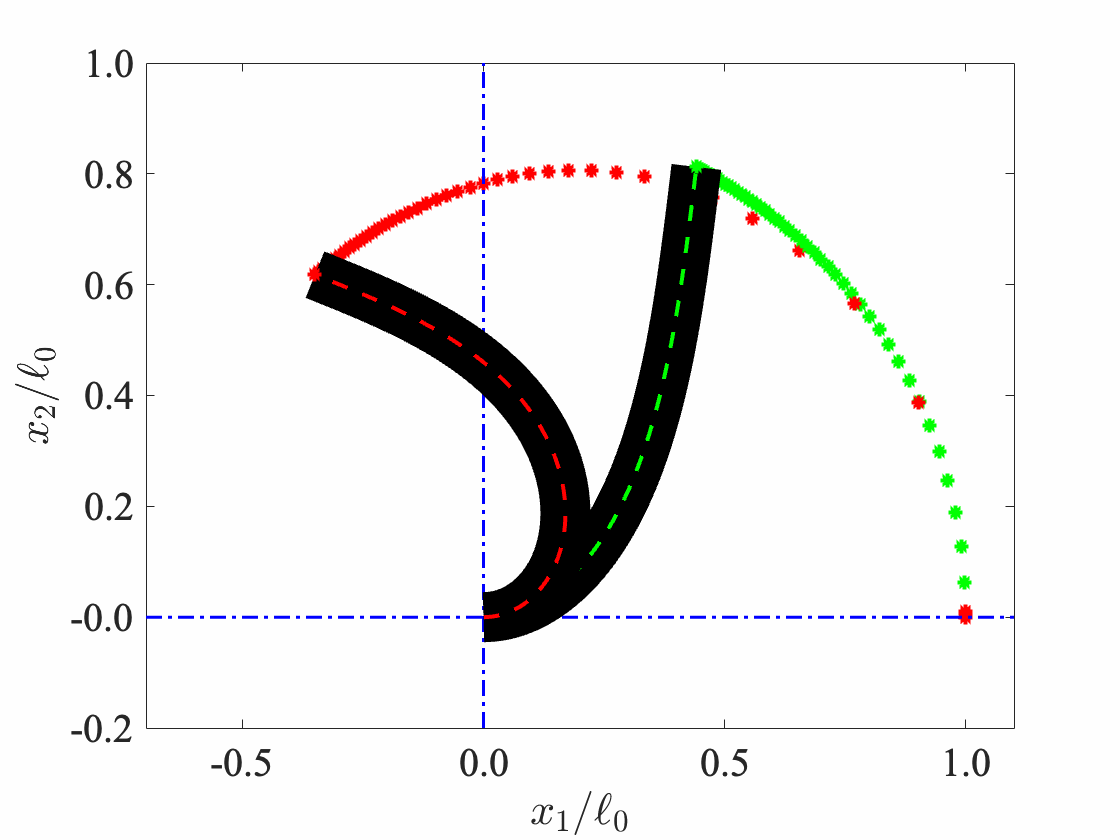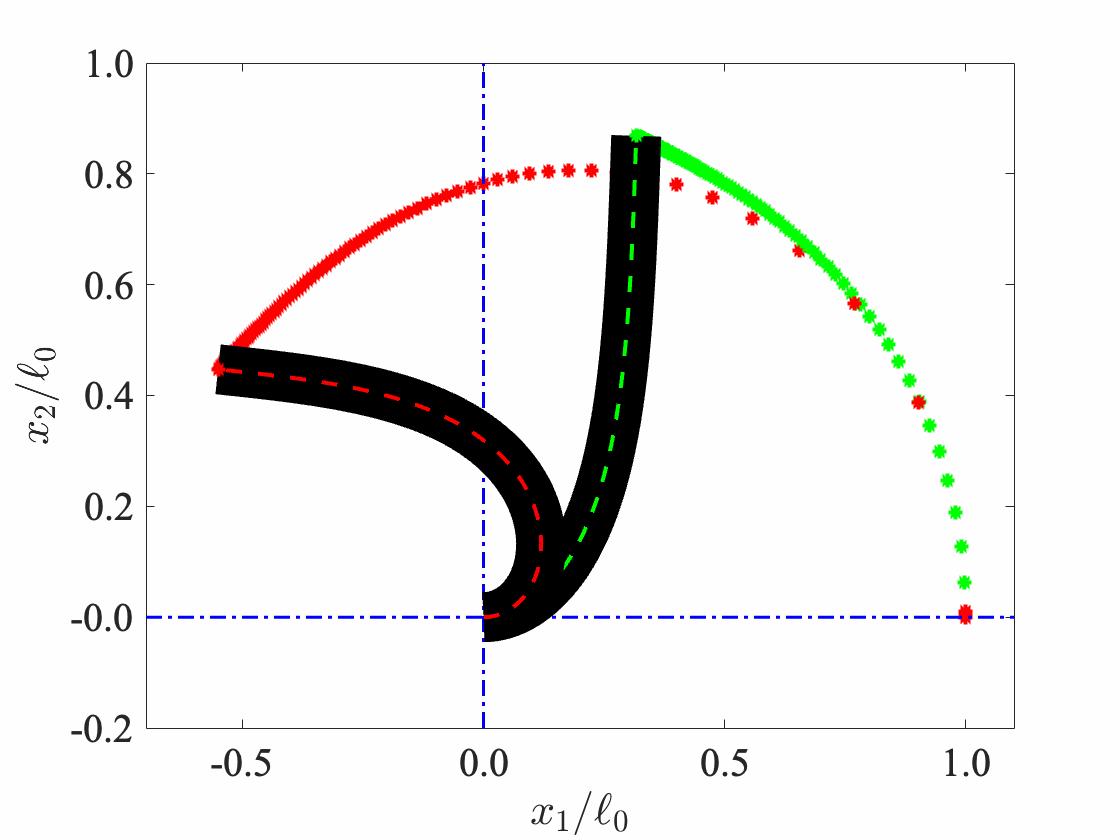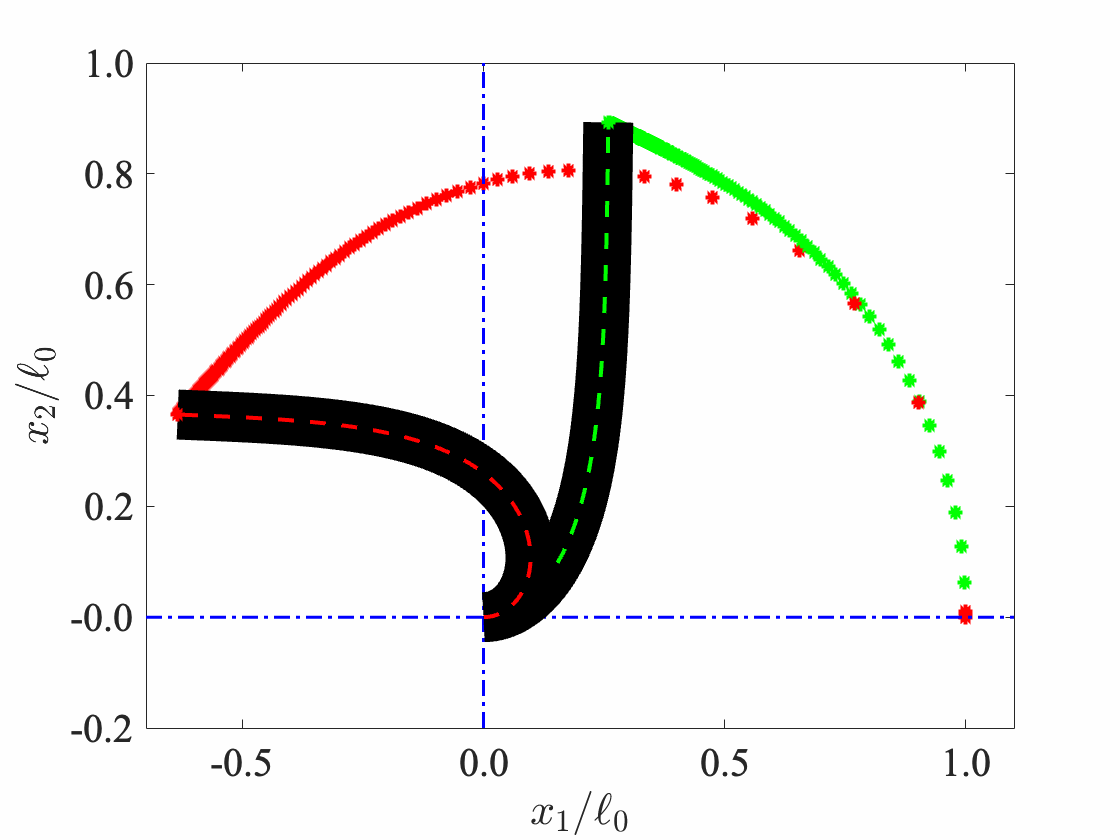
Geometrically-exact (GE) beam model, also referred as Cosserat rods, are typically employed to describe flexible slender continuum structures. I have employed the Simo-VuQuoc GE beam model in MATLAB. The details of implementation can be found in my thesis. The magnetic torque experienced by the GE beams is modelled following Pedro Rice’s model, which is inspired by the full-field continuum model in our IJSS paper.
MATLAB code folder: pre_mag_ge_beam.zip
Related courses taught in IITK: ME621A, ME623A, ME626A, ME676A.
-
2D dynamic simulation of geometrically-exact beams

The 2-dimensional dynamic simulation of GE beams is carried out following Simo-VuQuoc formulation. Please refer to my M.Tech. thesis for details of the modelling and MATLAB implementation. The MATLAB code folder is included in the following. Run the main file nlfem_dyn.m. The code is benchmarked against Simo-VuQuoc’s paper and also checked against Euler-Bernoulli beam model results under limiting conditions.
MATLAB code folder: 2D_dynamic_cosserat.zip
Related courses taught in IITK: ME621A, ME623A, ME626A, ME676A.